Building an exponential converter
In this article I’ll describe the steps I took to design an exponential converter. YMMV of course, but I think this article is a good start and may provide some useful guidelines.
The following table shows the relation between Hertz and wavelength. These are the MIDI C notes per octave, in Hz with their corresponding wavelength in ms
8.1757989156 hz 122.312205856 ms 16.3515978313 hz 61.156102927 ms 32.7031956626 30.578051464 65.4063913251 15.289025732 130.8127826503 7.644512866 261.6255653006 3.822256433 523.2511306012 1.911128216 1046.5022612024 0.955564108 2093.0045224048 0.477782054
The required wavelength a capable VCO should be able to deliver thus lays between 122ms and 0.47ms. Experimenting with a slightly customised sawtooth generator (design below) shows the following relation between the (ideal) current source and the wavelength.
0.1ua -> 470ms 1ua -> 47ms 10ua -> 4.7ms 100ua -> 0.47ms (470us) 1000ua (1ma)-> 0.047ms
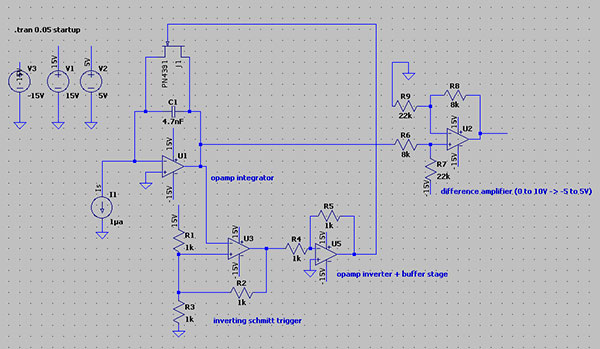
First, the slightly customised sawtooth VCO. The inverting Schmitt trigger in the sawtooth reset circuit guarantees a long enough reset pulse and thus a clean reset of the sawtooth waveform. The capacitor is too large, leading to a small distortion in the waveform. Will be fixed in updates.
The current source (exponential converter) must deliver a steady current between 0.1ua and 1000ua to the VCO to have to VCO achieve interesting musical abilities (enough octaves, very low frequencies, MIDI controllable). The deployment of an exponential converter in this current source is almost inevitable. Linear control, preferable digital through DAC’s or such, of a current source with such a bandwidth (0.1ua -> 1000ua) is very difficult.
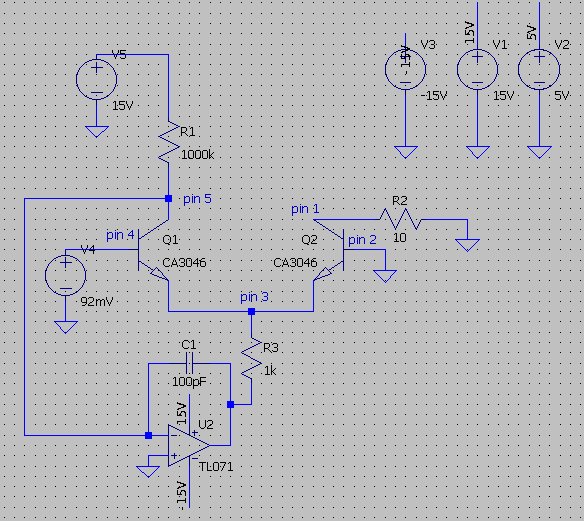
The circuit of the exponential converter:
The formula for the exponential part of the converter is iout = iref * exp(-Vb/Vt) where vt = 26mV.
iref runs over R1 => iref = Vref / Rref = 15V / 1000000ohm = 0.000015A = 15uA. To achieve an output current of 0.1ua (the VCO will generate a 470ms waveform) => 0.1 = 15 * exp(-Vb/26) => Vb = 130mV. Some calculations of Vb in the required bandwidth of 0.1ua and 1000ua:
wavelength: current -> required voltage 470: 0.1ua -> 130mV 235: 0.2ua -> 111mV 118: 0.4ua -> 94mV 59: 0.8ua -> 76mV 30: 1.6ua -> 58mV 15: 3.2ua -> 40mV 8: 5.9ua -> 24mV 4: 11.75ua -> 6mV 2: 24ua -> -12mV 1: 47ua -> -30mV 0.5: 94ua -> -48mV 0.25: 188ua -> -66mV
This leads to a relation between linear voltage and exponential current! Required to translate a difference of 1 volt to a musical difference of 1 octave (which is a exponential scale).
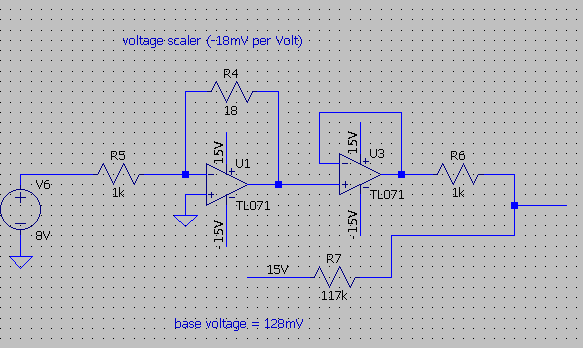
The voltage into the exponential converter will thus have a 1V/octave scaling and start at 0 volts (130mV) up to 12 volts (-66mV). The base voltage will be 130mV. The voltage scaling opamp will have to scale the incoming voltage (0-12V) to a -18mV per Volt. This voltage is buffered by an opamp follower and a voltage summer then combines the base voltage and the voltage scaler voltage (note to self: make the 1k in the summer smaller for a more precise summer).
The exponential converter takes this voltage (in V4) and transforms it into a current source following calculations above. Temperature drifting and transistor matching have not been explored in full. For now the CA3046 is deployed. Temperature compensation is probably achievable by driving the other transistors in the CA3046 to a certain temp (like in the Moog Prodigy).